how to find degrees of freedom

The degrees of freedom (DF) in statistics indicate the number of independent values that can vary in an analysis without breaking any constraints. It is an essential idea that appears in many contexts throughout statistics including hypothesis tests, probability distributions, and regression analysis. Learn how this fundamental concept affects the power and precision of your analysis!

In this blog post, I bring this concept to life in an intuitive manner. I'll start by defining degrees of freedom and providing the formula. However, I'll quickly move on to practical examples in the context of various statistical analyses because they make this concept easier to understand.

Definition of Degrees of Freedom

What are degrees of freedom in statistics? Degrees of freedom are the number of independent values that a statistical analysis can estimate. You can also think of it as the number of values that are free to vary as you estimate parameters. I know, it's starting to sound a bit murky!

DF encompasses the notion that the amount of independent information you have limits the number of parameters that you can estimate. Typically, the degrees of freedom equals your sample size minus the number of parameters you need to calculate during an analysis. It is usually a positive whole number.

Degrees of freedom is a combination of how much data you have and how many parameters you need to estimate. It indicates how much independent information goes into a parameter estimate. In this vein, it's easy to see that you want a lot of information to go into parameter estimates to obtain more precise estimates and more powerful hypothesis tests. So, you want many DF!

Independent Information and Constraints on Values

The degrees of freedom definitions talk about independent information. You might think this refers to the sample size, but it's a little more complicated than that. To understand why, we need to talk about the freedom to vary. The best way to illustrate this concept is with an example.

Suppose we collect the random sample of observations shown below. Now, imagine we know the mean, but we don't know the value of an observation—the X in the table below.

Data table to illustrate degrees of freedom when calculating the mean.

The mean is 6.9, and it is based on 10 values. So, we know that the values must sum to 69 based on the equation for the mean.

Using simple algebra (64 + X = 69), we know that X must equal 5.

Related post: What is the Mean in Statistics?

How to Find the Degrees of Freedom in Statistics

As you can see, that last number has no freedom to vary. It is not an independent piece of information because it cannot be any other value. Estimating the parameter, the mean in this case, imposes a constraint on the freedom to vary. The last value and the mean are entirely dependent on each other. Consequently, after estimating the mean, we have only 9 independent pieces of information, even though our sample size is 10.

That's the basic idea for degrees of freedom in statistics. In a general sense, DF are the number of observations in a sample that are free to vary while estimating statistical parameters. You can also think of it as the amount of independent data that you can use to estimate a parameter.

Degrees of Freedom Formula

The formula for finding the degrees of freedom is straightforward. The degrees of freedom equals the sample size minus the number of parameters you're estimating:

DF = N – P

Where:

N = sample size
P = the number of parameters or relationships

For example, the degrees of freedom for a 1-sample t test equals N – 1 because you're estimating one parameter, the mean.

The formula for calculating degrees of freedom for a table in a chi-square test is (r-1) (c-1), where r = the number of rows and c = the number of columns.

DF and Probability Distributions

Degrees of freedom also define the probability distributions for the test statistics of various hypothesis tests. For example, hypothesis tests use the t-distribution, F-distribution, and the chi-square distribution to determine statistical significance. Each of these probability distributions is a family of distributions where the DF define the shape. Hypothesis tests use these distributions to calculate p-values. So, the DF directly link to p-values through these distributions!

Next, let's look at how these distributions work for several hypothesis tests.

Related posts: Understanding Probability Distributions and A Graphical Look at Significance Levels (Alpha) and P values

Degrees of Freedom for t Tests and the t-Distribution

T tests are hypothesis tests for the mean and use the t-distribution to determine statistical significance.

A 1-sample t test determines whether the difference between the sample mean and the null hypothesis value is statistically significant. Let's go back to our example of the mean above. We know that when you have a sample and estimate the mean, you have n – 1 degrees of freedom, where n is the sample size. Consequently, for a 1-sample t test, the degrees of freedom equals n – 1.

The DF define the shape of the t-distribution that your t-test uses to calculate the p-value. The graph below shows the t-distribution for several different degrees of freedom. Because the degrees of freedom are so closely related to sample size, you can see the effect of sample size. As the DF decreases, the t-distribution has thicker tails. This property allows for the greater uncertainty associated with small sample sizes.

The degrees of freedom chart below displays t-distributions.

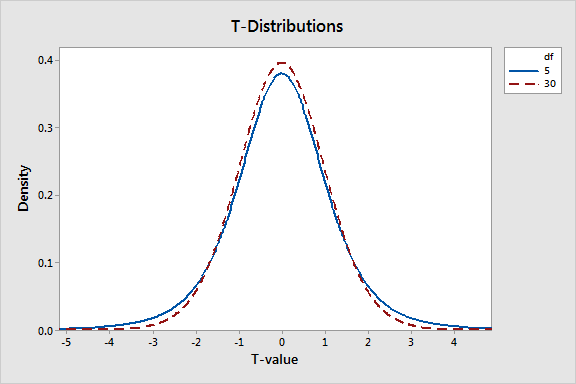
Graph that compares shape of t-distributions with 5 and 30 degrees of freedom.

To dig into t-tests, read my post about How t-Tests Work. I show how the different t-tests calculate t-values and use t-distributions to calculate p-values.

The F-test in ANOVA also tests group means. It uses the F-distribution, which is defined by the DF. However, you calculate the ANOVA degrees of freedom differently because you need to find the numerator and denominator DF. For more information, read my post about How F-tests Work in ANOVA.

You'll often find degrees of freedom in tables along with their critical values. Statisticians look up DF in these tables to determine whether the test statistic for their hypothesis test falls in the critical region, indicating statistical significance.

Related post: How to Interpret P-values Correctly

Degrees of Freedom for Tables in Chi-Square Tests

The chi-square test of independence determines whether there is a statistically significant relationship between categorical variables in a table. Just like other hypothesis tests, this test incorporates DF. For a table with r rows and c columns, the formula for finding the degrees of freedom for a chi-square test is (r-1) (c-1).

However, we can create tables to understand how to find their degrees of freedom more intuitively. The DF for a chi-square test of independence is the number of cells in the table that can vary before you can calculate all the other cells. In a chi-square table, the cells represent the observed frequency for each combination of categorical variables. The constraints are the totals in the margins.

Chi-Square 2 X 2 Table

For example, in a 2 X 2 table, after you enter one value in the table, you can calculate the remaining cells.

A 2 by 2 table to illustrate degrees of freedom for a chi-square test of independence.

In the table above, I entered the bold 15, and then I can calculate the remaining three values in parentheses. Therefore, this table has 1 DF.

Chi-Square 3 X 2 Table

Now, let's try a 3 X 2 table. The table below illustrates the example that I use in my post about the chi-square test of independence. In that post, I determine whether there is a statistically significant relationship between uniform color and deaths on the original Star Trek TV series.

A 3 by 2 table to illustrate the degrees of freedom for a chi-square test of independence.

In the table, one categorical variable is shirt color, which can be blue, gold, or red. The other categorical variable is status, which can be dead or alive. After I entered the two bolded values, I can calculate all the remaining cells. Consequently, this table has 2 DF.

Read my post, Chi-Square Test of Independence and an Example, to see how this test works and how to interpret the results using the Star Trek example.

Like the t-distribution, the chi-square distribution is a family of distributions where the degrees of freedom define the shape. Chi-square tests use this distribution to calculate p-values. The degrees of freedom chart below displays several chi-square distributions.

Graph that displays the distribution of chi-squared based on different degrees of freedom.

Degrees of Freedom in Regression Analysis

Finding the degrees of freedom in regression is a bit more complicated, and I'll keep it on the simple side. Think back to the general formula for DF, N – P. In a regression model, each term is an estimated parameter that uses one degree of freedom. In the regression output below, you can see how each term requires a DF. There are 28 observations and the two independent variables use a total of two DF. The output displays the remaining 26 degrees of freedom in Error.

ANOVA table that shows the degrees of freedom for regression analysis.

The error DF are the independent pieces of information that are available for estimating your coefficients. For precise coefficient estimates and powerful hypothesis tests in regression, you must have many error degrees of freedom, which equates to having many observations for each model term.

As you add terms to the model, the error degrees of freedom decreases. You have fewer pieces of information available to estimate the coefficients. This situation reduces the precision of the estimates and the power of the tests. When you have too few remaining DF, you can't trust the regression results. If you use all your degrees of freedom, the procedure can't calculate the p-values.

For more information about the problems that occur when you use too many DF and how many observations you need, read my blog post about overfitting your model.

Even though they might seem murky, degrees of freedom are essential to any statistical analysis! In a nutshell, DF define the amount of information you have relative to the number of properties that you want to estimate. If you don't have enough data for what you want to do, you'll have imprecise estimates and low statistical power.

References

Walker, H. W. Degrees of Freedom. Journal of Educational Psychology. 31(4) (1940) 253-269.

Pandy, S., and Bright, C. L., Social Work Research Vol 32, number 2, June 2008.